A nation uses energy to maintain its defenses. Every defense that a nation builds costs a certain amount of energy each hour to maintain, and a nation generates energy continuously. It’s important to avoid building so many defenses that your nation burns more energy each hour than it generates; if this happen, you won’t be able to maintain all of your defenses and some will become inert and ineffective.
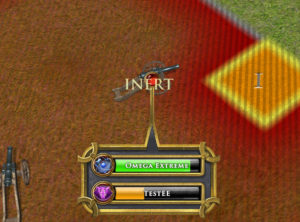
Attacking an inert defense
The rate at which a nation generates energy is determined by its Energy Generation Rate stat. A new nation generates 310 energy per hour, and the Energy Generation Rate can be increased by researching advances and by capturing certain resources.
The total cost to maintain all of a nation’s defenses each hour is called the nation’s Energy Burn Rate. This is a stat that can be viewed under the Nation Panel’s Stats tab. If the Energy Burn Rate exceeds the Energy Generation Rate, then the nation will not be able to support all of its defenses and some will become inert. Your nation’s inert defenses will appear to you in red, but other nations’ players will not be able to tell which of your defenses are inert until they attack. When attacked, an inert defense will fail to trigger; instead, it will emit a puff of smoke and the word “inert” will appear over it, letting the attacker know that it is out of commission.
The greater the amount that a nation’s Energy Burn Rate exceeds its Energy Generation Rate, the more an “overburn” penalty applies, which causes the Energy Burn Rate to shoot up exponentially. So, while a nation that generates enough energy to cover 90% of the energy cost of its defenses will only have about 10% of its defenses become inert, a nation that generates only enough energy to cover 50% of its defenses will see much more than 50% of its defenses become inert.
There is, however, a buffer that a nation has, to allow it to briefly spend more energy on its defenses than it generates. This buffer is the nation’s Energy Reserves stat. While a nation is generating more energy than its defenses burn, its Energy Reserves fill up. Then, the nation can use those reserves to build more defenses and temporarily burn energy more quickly than it is generated. Only once the reserves run out will defenses begin to become inert. A nation can increase the total amount of energy it can store in reserve by developing advances that boost its Max Energy. Note that a nation’s energy reserves only apply on the mainland game world; there are no energy reserves on a nation’s home island or during a raid, so burning more energy than is generated there will immediately result in some defenses becoming inert.

The Energy Bar
The blue Energy Bar in the upper right corner of the screen will keep you informed about how much energy your nation is generating versus how much it is burning. This bar shows the amount being generated minus the amount being burned, per hour. If the bar is full, your nation has built no defenses and is burning none of the energy that it generates. If the bar reaches empty, however, your nation is burning all of its energy as fast as it generates it. Ideally you’ll want to keep this bar slightly above zero, to avoid allowing defenses to become inert.
On the mainland map the Energy Bar also shows, in lighter blue, how full your nation’s energy reserves are. For example, in the image above, the energy bar shows that the nation is burning about 2/3 of the energy it is generating (because the deep blue bar is only 1/3 full) leaving an excess of 80. The light blue bar shows that the nation’s energy reserves are about 75% full.
If your nation’s energy reserves are less than full, you can buy more energy for your reserves by spending credits. After you’ve bought 100% of your nation’s max Energy Reserves worth of energy in one day, you will not be able to buy any more until the next day.
Next: Geographic Efficiency

Recent Comments